Gaussian Splatting: A Deep Dive into Transforming 3D Data for Real-Time Visualization
Introduction
In the vast domain of computer graphics, transforming complex 3D models into 2D images for visualization, analysis, or further processing is a fundamental challenge. One of the most efficient and visually accurate methods to achieve this transformation is through a technique known as Gaussian splatting. This blog post delves into the essence of Gaussian splatting, introduces a pioneering SIGGRAPH paper 3D Gaussian Splatting for Real-Time Rendering of Radiance Fields, and explores the gsplat library—an open-source toolkit designed to implement these concepts with modern technology.
What is Gaussian Splatting?
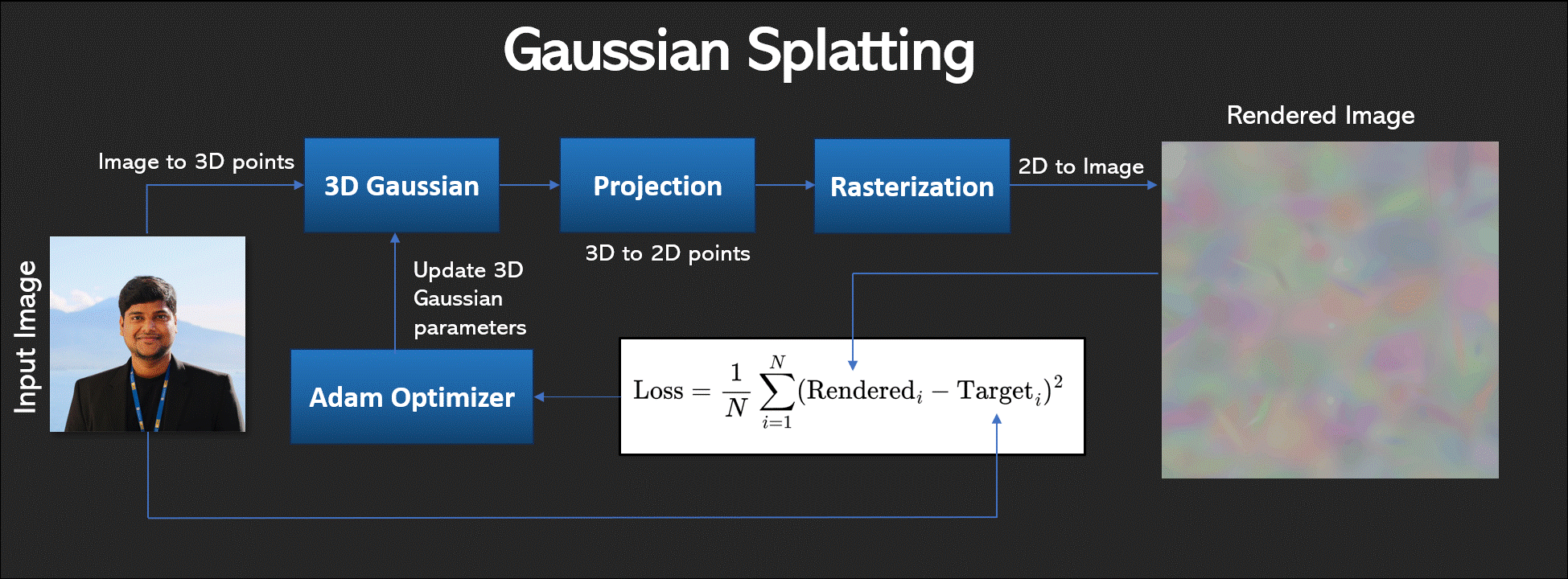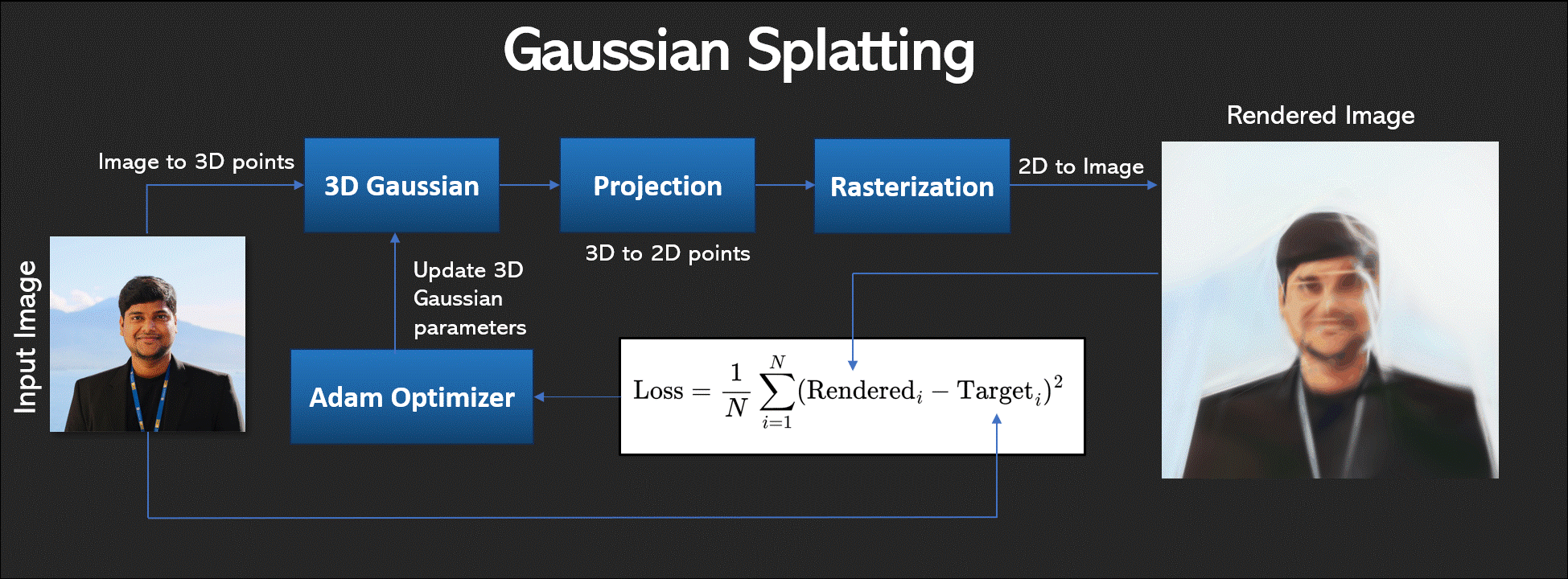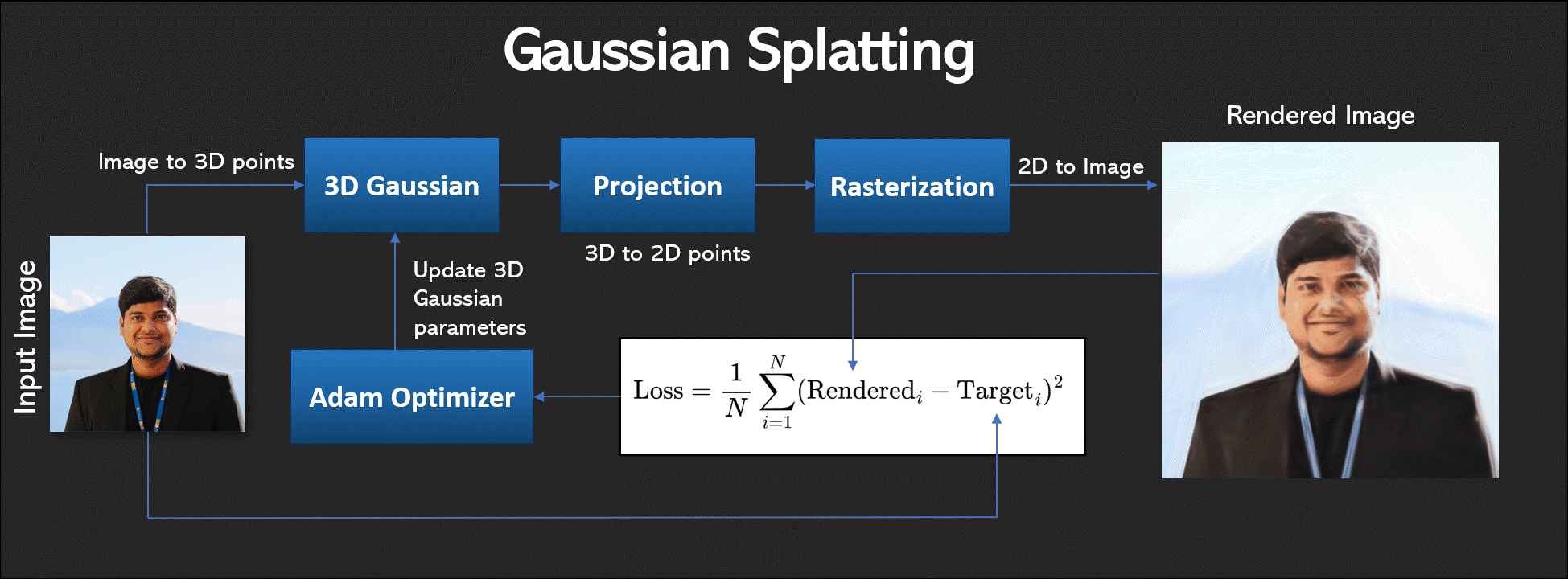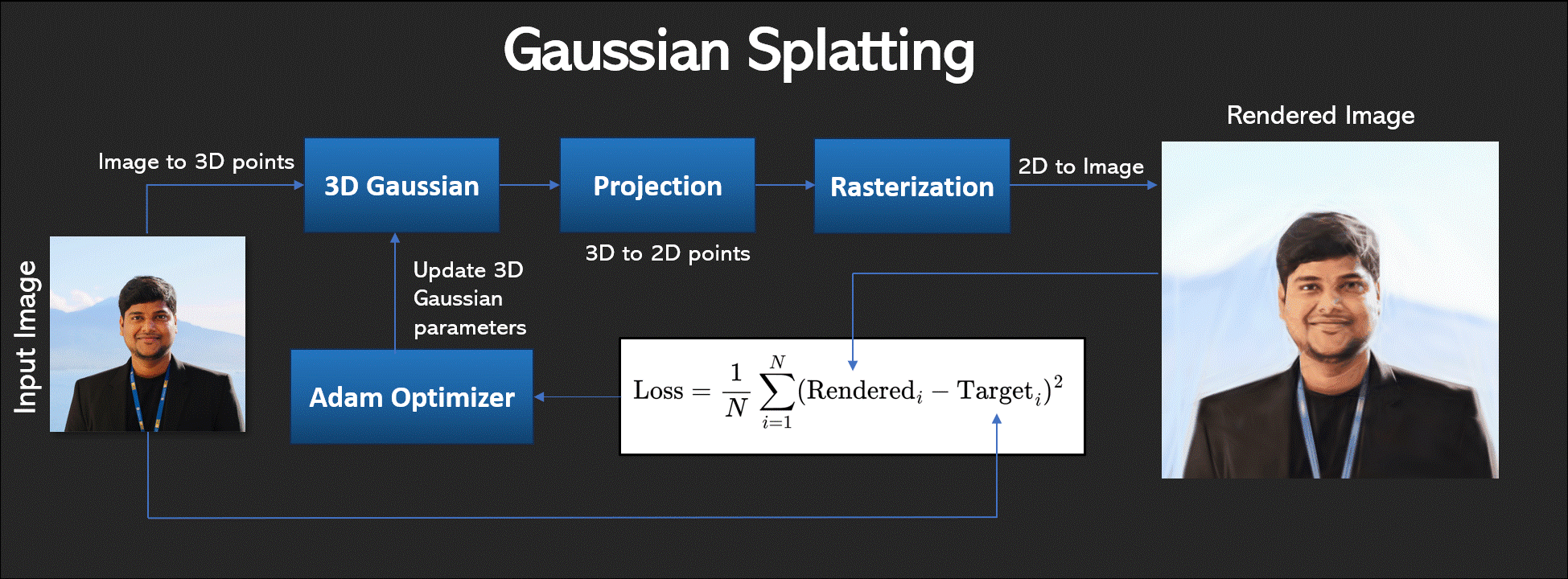
Gaussian splatting is a rendering technique used to project 3D data onto a 2D plane by representing each data point as a Gaussian function. This method is particularly useful in volume rendering and point cloud visualization. The core idea is to “splat” each 3D point onto the 2D canvas, where it spreads its influence according to its Gaussian distribution, blending with other points to create a cohesive image.
The Detailed Process of Gaussian Splatting and Rendering
The transformation from 3D Gaussians to a 2D representation involves several steps, each underpinned by mathematical principles. Let’s explore these steps in detail.
Step 1: Representing 3D Points as Gaussians
Each point in a 3D model is represented by a Gaussian function, characterized by a mean \(\mu\) (the point’s location in 3D space) and a covariance matrix \(\Sigma\) (determining the spread of the point).
Step 2: Camera Transformation
3D points must first be transformed to the camera coordinate system using the camera’s extrinsic parameters matrix \(T_{cw}\):
\[t = T_{cw} \cdot \begin{pmatrix} \mu \\ 1 \end{pmatrix}\]This matrix, \(T_{cw}\), encapsulates the camera’s position and orientation in space, effectively aligning 3D model points (\(\mu\)) with the camera’s viewpoint.
Step 3: Perspective Projection
Next, The transition of 3D points to a 2D plane leverages the camera’s intrinsic properties, defined by the projection matrix \(P\):
\[P = \begin{bmatrix} \frac{2f_x}{w} & 0 & 0 & 0 \\ 0 & \frac{2f_y}{h} & 0 & 0 \\ 0 & 0 & \frac{f + n}{f - n} & \frac{-2fn}{f - n} \\ 0 & 0 & 1 & 0 \end{bmatrix}\]Here, \(f_x\) and \(f_y\) are the camera’s focal lengths, \(w\) and \(h\) denote the viewport’s width and height, and \(n\) and \(f\) represent the near and far clipping planes, respectively. This matrix transforms 3D coordinates to normalized device coordinates (NDC), subsequently adjusted to 2D pixel coordinates \(\mu'\) through viewport transformations.
Step 4: Depth Compositing and Rasterization
Once 3D points are projected onto the 2D plane as Gaussians, accurately rendering these points requires a sophisticated approach known as depth compositing followed by rasterization. This process ensures that each Gaussian’s contribution to the final image is calculated considering its depth, allowing for realistic blending and occlusion effects.
Depth Sorting
The first task in depth compositing is to sort the Gaussians based on their depth from the camera’s perspective. This sorting ensures that Gaussians closer to the camera are processed before those farther away, which is critical for correctly applying transparency and occlusion:
\[\text{Depth Sorted Gaussians} = \text{Sort}(\text{Gaussians}, \text{by Depth})\]Gaussian Rasterization
Rasterization converts these sorted Gaussians into pixel values on the 2D image. For each Gaussian, its influence on a pixel is determined by its distance from the pixel center, modeled by the Gaussian’s spread (\(\Sigma'\)) in 2D space. The contribution of a Gaussian to a pixel’s color \((C_i)\) and opacity \((\alpha)\) is calculated using its 2D projected parameters:
\[C_i = \sum_{n \leq N} c_n \cdot \alpha_n \cdot T_n, \quad \alpha_n = o_n \cdot \exp\left(-\frac{1}{2} \Delta_n^T \Sigma'^{-1} \Delta_n\right)\]where \(c_n\) is the color of the nth Gaussian, \(o_n\) its opacity, \(\Delta_n\) the distance from the pixel center to the Gaussian’s center, and \(T_n\) accounts for the cumulative transparency of all Gaussians in front of it.
Training with Gradient Descent
The gsplat library facilitates the inverse rendering process, allowing for the optimization of 3D Gaussian parameters to minimize the discrepancy between a rendered image and a target image. This is achieved through a gradient descent approach, iterating through the following steps:
Forward Pass: Rendering the Image
Initially, the 3D Gaussians are projected and rasterized to form a 2D image as described in Steps 1 through 4. This image represents the current state of the 3D model as seen from the camera’s perspective.
Loss Calculation: Quantifying the Difference
A loss function quantifies the difference between the rendered image and the target image. The Mean Squared Error (MSE) is often used for its simplicity and effectiveness:
\[\text{Loss} = \frac{1}{N} \sum_{i=1}^{N} (\text{Rendered}_i - \text{Target}_i)^2\]Backward Pass: Computing Gradients
To adjust the 3D Gaussians to reduce this loss, the gradient of the loss with respect to each parameter of the Gaussians (mean, covariance, color, opacity) is computed. This involves differentiating through the rendering process, a non-trivial task made feasible by the differentiable nature of the gsplat library’s operations.
Parameter Update: Applying Gradient Descent
Using the computed gradients, the parameters of the 3D Gaussians are updated in the direction that reduces the loss. The learning rate (\(\eta\)) controls the size of these updates:
\[\theta_{\text{new}} = \theta_{\text{old}} - \eta \cdot \nabla_{\theta} \text{Loss}\]where \(\theta\) represents the parameters of the Gaussians.
Psuedo Code for training Gaussian Splating
Trainer Class Overview
- Initialization:
- Load and store the ground truth image.
- Define the number of 3D Gaussian points.
- Calculate the camera’s focal length from image dimensions and field of view.
-
_init_gaussians().
- _init_gaussians() Method:
- Randomly initialize the means, scales, and RGB colors of 3D Gaussians.
- Generate random quaternions for Gaussian rotation.
- Set all Gaussians’ opacities to 1.
- Define the camera’s view matrix and background color.
- Enable gradient computation for all Gaussian parameters.
- train() Method:
- Set up an optimizer (e.g., Adam) for the Gaussian parameters.
- Define a loss function (e.g., mean squared error) for training.
- For each training iteration:
- Project 3D Gaussians to 2D space, considering camera settings.
- Rasterize projected 2D Gaussians, blending colors and opacities based on depth.
- Calculate the loss between the rendered image and the target image.
- Compute gradients of the loss with respect to Gaussian parameters and update them.
Get the Code Here
Reference
- https://github.com/nerfstudio-project/gsplat/
- hKerbl, Bernhard, et al. “3D Gaussian Splatting for Real-Time Radiance Field Rendering.” ArXiv, 2023, /abs/2308.04079. Accessed 20 Mar. 2024.
- Ye, Vickie, and Angjoo Kanazawa. “Mathematical Supplement for the $\Texttt{Gsplat}$ Library.” ArXiv, 2023, /abs/2312.02121. Accessed 20 Mar. 2024.