Why Large Language Models Fail at Precision Regression
1. Introduction
Large Language Models (LLMs) such as OpenAI o3, DeepSeek-R1, LLaMA, and other Transformer based architectures have revolutionized natural language processing. They exhibit impressive capabilities in generating text, summarizing lengthy articles, answering questions, and even demonstrating a form of “reasoning” about numerical problems. However, a significant limitation persists: LLMs often fail when required to produce precise numerical outputs.
This limitation isn’t just a small flaw. It’s a fundamental consequence of their architecture and training methodologies. In fields like financial forecasting, engineering simulations, and scientific data analysis, where outputs frequently demand decimal level or even floating point precision, even tiny numerical errors can lead to substantial real world consequences, such as underestimating financial risk or miscalculating critical engineering parameters.
The reasons for this inherent imprecision can be summarized as follows:
- Tokenization Barrier: LLMs represent text as sequences of discrete tokens. When applied to numbers, continuous real values are discretized into a finite set of symbols or subwords. Even with a fine-grained numeric vocabulary, this token level representation introduces quantization errors that are unavoidable.
- Autoregressive Compounding: LLMs generate text (and thus numbers) one token at a time, based on preceding tokens. If the model mis-predicts a token (e.g., getting one decimal place wrong), subsequent tokens can be thrown off, leading to error accumulation, especially when many digits or decimal places are required.
- Smoothness vs. Discreteness: Traditional regression tasks (predicting a real value \(y \in \mathbb{R}\)) typically benefit from smooth real valued functions. In contrast, the output of LLMs is discrete, creating discontinuities that restrict accurate mapping from input \(x\) to numeric output \(f(x)\).
- Bias-Variance Trade-off: LLMs exhibit high bias due to systematic discretization error and high variance due to token by token randomness.
The key takeaway is that LLMs are fundamentally designed to work with text, which is discrete. Representing continuous numbers with discrete tokens introduces unavoidable errors.
For a detailed mathematical analysis of these limitations, including proofs and formal definitions, continue to the next section. The following section explores how tokenization, autoregressive decoding, and discrete outputs contribute to the inherent challenges LLMs face in achieving precise numerical regression.
2. Theoretical Analysis
2.1 Tokenization \(\implies\) Irreducible Quantization Error
LLMs’ numeric outputs must undergo a tokenization process, meaning that instead of representing numbers with infinite precision, they are approximated using a finite set of discrete symbols (tokens). This tokenization introduces a fundamental limitation: quantization error. To illustrate this, consider the following example:
Suppose we want to represent real numbers in the range. We can divide this range into ten equal sub-intervals and assign a unique token to each sub-interval:
- \([0, 0.1)\) → Token “0.0”
- \([0.1, 0.2)\) → Token “0.1”
- \([0.2, 0.3)\) → Token “0.2”
- \([0.3, 0.4)\) → Token “0.3”
- \([0.4, 0.5)\) → Token “0.4”
- \([0.5, 0.6)\) → Token “0.5”
- \([0.6, 0.7)\) → Token “0.6”
- \([0.7, 0.8)\) → Token “0.7”
- \([0.8, 0.9)\) → Token “0.8”
- \([0.9, 1]\) → Token “1.0”
Each sub-interval follows a left-closed, right-open format (e.g., \([0.1, 0.2)\)), meaning that the lower boundary is included, but the upper boundary belongs to the next interval. The only exception is the last interval, \([0.9, 1]\), which is fully closed to include the upper bound.
In this setup, every real number within a given sub-interval is represented by the same token. For example, any number between \(0\) and \(0.1\) will be represented by the token “0.0”. This means we lose the ability to distinguish between values within that interval.
The inability to pinpoint exact values due to tokenization leads to quantization error. To formalize this concept, we can state the following lemma:
Lemma (Finite Tokenization Bound)
Statement: Suppose \([a,b] \subset \mathbb{R}\) is partitioned into intervals \(I_k\), each of diameter \(\delta\). If \(T\) maps each interval to a unique token, then:
\[\sup_{y\in[a,b]} | T^{-1}(T(y)) - y | \geq \frac{\delta}{2}.\]In other words, when mapping a continuous range to discrete tokens, a minimum reconstruction error of \(\frac{\delta}{2}\) is unavoidable.
Explanation:
- \([a,b]\): Represents a closed interval on the real number line.
- \(I_k\): Denotes the set of sub-intervals that partition \([a,b]\).
- \(\delta\): Represents the diameter (width) of each sub-interval \(I_k\).
- \(T\): A tokenization function that maps each sub-interval to a unique token.
- \(T^{-1}\): The inverse function of \(T\), which maps a token back to its corresponding sub-interval.
- \(y\): A real number within the interval \([a,b]\).
- The expression: \(| T^{-1}(T(y)) - y |\) represents the absolute difference between the original real number \(y\) and the value obtained by tokenizing \(y\) and then mapping it back to its sub-interval.
- The supremum \(\sup_{y\in[a,b]}\): Finds the largest possible value of this absolute difference over all real numbers \(y\) in the interval.
Example:
Let’s say we divide the interval into ten equal parts as shown above (with a width of 0.1). If we want to represent the number 0.35, it falls into the interval [0.3, 0.4), which corresponds to the token “0.3”. However, we cannot differentiate between any value in that interval, whether it’s 0.31 or 0.39 all are represented by the same token.
The maximum error occurs when a true value is exactly halfway between two tokens (e.g., at 0.35). In this case, since our nearest tokens are “0.3” and “0.4”, we can have an error of up to ± 0.05 (which is half of our interval width).
Key Takeaway
This lemma illustrates a fundamental limitation: even if an LLM had a perfect internal representation of a real number, mapping that number to tokens introduces an unavoidable baseline error of at least \(\frac{\delta}{2}\). No amount of training or model complexity can eliminate this quantization error. It is an inherent characteristic of using discrete tokens for continuous values.
2.2 Autoregressive Decoding \(\implies\) Error Accumulation
When an LLM generates a multi-token numeric output—e.g., a five-digit decimal “3.1415” it does so one token at a time. The correctness of each token influences the distribution over subsequent tokens. This sequential nature introduces a fundamental issue: error accumulation.
Why Does Error Accumulate?
LLMs generate outputs autoregressively, meaning they predict each token based on the tokens that came before it. If an error occurs early in the sequence (e.g., predicting “3.142” instead of “3.141”), it shifts the probability distribution for all subsequent tokens, making further mistakes more likely.
This phenomenon is particularly problematic for numbers because numeric precision depends on every single digit being correct. Unlike natural language, where minor word level errors may still preserve meaning, even a small deviation in a numeric sequence can lead to a completely different result.
Theorem: Error Accumulation in Autoregressive Decoding
Statement: Let \(\hat{y} = (y_1, y_2, \dots, y_n)\) be an \(n\) token sequence representing a real number \(y\). Suppose each step incurs:
- A quantization error \(\epsilon_T\) (due to tokenization limitations)
- A modeling error \(\epsilon_M(i)\) (due to imperfect conditional predictions)
Then, the expected overall error is lower-bounded as:
\[\mathbb{E}\Bigl[|T^{-1}(\hat{y}) - y|\Bigr] \geq \sum_{i=1}^{n} \bigl[\epsilon_T + \epsilon_M(i)\bigr] - O(1).\]This implies that as the number of tokens \(n\) increases (i.e., more digits are required for precision), the total numeric error increases proportionally.
- \(\hat{y}\): The predicted numeric sequence, represented as a sequence of tokens.
- \(y_i\): The \(i\)-th token in the predicted sequence.
- \(y\): The actual real number that the model is attempting to generate.
- \(\epsilon_T\): Quantization error arising from discretization of continuous numbers into tokens.
- \(\epsilon_M(i)\): Modeling error at the \(i\)-th token due to imperfect predictions.
- \(T^{-1}(\hat{y})\): The function that maps token sequences back to real values.
- \(\mathbb{E}[\cdot]\): The expectation operator, representing the expected error over multiple predictions.
- \(O(1)\): A notation indicating that the term is bounded and does not grow with \(n\).
Explanation
- Tokenization introduces unavoidable baseline errors (\(\epsilon_T\)):
- Just like in Section 2.1, tokenization discretizes continuous values, causing some inherent precision loss.
- Even if the model were perfect, this quantization error cannot be removed.
- Autoregressive models introduce sequential dependency errors (\(\epsilon_M(i)\)):
- Each token prediction depends on previous tokens.
- If an early digit is incorrect, later digits are conditioned on an already incorrect prefix.
- This means that errors from earlier digits can propagate and amplify as more tokens are generated.
- Error grows with longer numeric sequences:
- Because each token can introduce an independent error term (\(\epsilon_M(i)\)), the overall expected error is at least the sum of these errors over all tokens.
- As more tokens are needed (e.g., higher precision decimals), total error increases.
Example
Imagine an LLM is being used in a clinical setting to assist with drug dosage calculations. The correct dosage for a patient should be “2.875 mg”, but let’s analyze what happens when a small early mistake occurs:
- Step 1: The model correctly predicts “2.”
- Step 2: Instead of “8”, the model predicts “9”, slightly increasing the dose.
- Step 3: Now, because the model believes the number is “2.9_“, it adjusts the probabilities for the next digit, increasing the likelihood of further deviations.
- Step 4: The cascading effect results in a final output of “2.964 mg” instead of “2.875 mg”, leading to an overdose risk.
A minor numerical error in an early digit caused a systematic shift in all subsequent values, leading to an incorrect dosage recommendation. In high-stakes fields like medicine, even a 0.1 mg deviation in certain drugs (e.g., anesthesia, insulin, or chemotherapy) could be life-threatening.
Key Takeaway
Thus, even if an LLM were trained on perfect mathematical data, its sequential generation process ensures that precise numeric outputs will always be prone to compounding errors. Because each token conditions future predictions, small errors get amplified across long outputs. This makes it inherently difficult for LLMs to maintain high-precision numeric accuracy over multiple tokens.
2.3 Discrete Decoding \(\implies\) Discontinuities
Because each token corresponds to a specific discrete label, the mapping from \(\mathcal{X} \to \hat{y}\) is inherently stepwise rather than smooth.
Traditional regression tasks involve continuous functions where small changes in input lead to small changes in output. However, LLMs use discrete tokenization, which can cause abrupt jumps whenever the target value crosses a token boundary.
Proposition (Discrete Output Jumps)
Statement: Suppose \(f^*(x)\) is a continuous function over \(x \in \mathcal{X}\), and \(\hat{f}(x)\) is an LLM-based function mapping \(x\) to discrete tokens in \(\mathcal{V}\). Then for any point where \(f^*(x)\) crosses a boundary between adjacent tokens:
\[\bigl|\hat{f}(x_1) - \hat{f}(x_2)\bigr| \geq \Delta\]for arbitrarily close values \(x_1, x_2\), where \(\Delta > 0\) is the discrete “gap” imposed by the tokenization.
- \(f^*(x)\): The true continuous function representing the ideal numeric mapping.
- \(\hat{f}(x)\): The LLM’s discrete approximation of \(f^*(x)\).
- \(x_1, x_2\): Two arbitrarily close input values.
- \(\mathcal{X}\): The input space from which \(x\) is drawn.
- \(\mathcal{V}\): The finite vocabulary of discrete tokens used by the LLM.
- \(\Delta\): The minimum discrete step size between tokenized outputs.
Explanation
- Token Boundaries: Each discrete token represents a range of values. When the true function crosses one of these boundaries, the LLM’s output jumps from one token to the next, causing a discontinuity.
- Stepwise Approximation: Even if the true function \(f^*(x)\) varies smoothly, the LLM’s discrete token-based approximation results in stepwise behavior.
Example
Suppose an LLM is used to predict interest rates based on customer financial data. The true function might predict a rate of 4.999%, but because LLMs tokenize numbers in fixed increments (e.g., “4.99%” and “5.00%” as separate tokens), the model might jump directly from 4.99% to 5.00% instead of smoothly increasing.
This seemingly small jump could have significant real-world consequences. In financial applications, a 0.01% difference in interest rates can alter loan payments, affecting affordability for consumers and risk assessments for banks.
Experiment: Token Boundary Effects in Embeddings
To empirically verify this discontinuity, we measured cosine distances between numerically adjacent embeddings using OpenAI text-embedding-ada-002 model. The results show abrupt jumps when crossing token boundaries, while smoothly varying numbers maintain proportional distances. For example, the cosine distance between 6.999 and 7.000 is 0.1256, nearly double that of 6.500 and 6.501 (0.0714), despite both pairs differing by 0.001. Similar discontinuities occur at 9.999 → 10.000 and 99.999 → 100.000, reinforcing that these jumps are specific to tokenization effects rather than natural numerical variation.
The following table summarizes the measured cosine distances:
| Number Pair | Cosine Distance |
|---|---|
| 6.999 vs. 7.000 | 0.1256 |
| 9.999 vs. 10.000 | 0.1274 |
| 99.999 vs. 100.000 | 0.1333 |
| 6.500 vs. 6.501 | 0.0714 |
| 9.500 vs. 9.501 | 0.0717 |
| 99.500 vs. 99.501 | 0.0657 |
In contrast, numbers that do not cross boundaries, such as 6.500 → 6.501, exhibit smaller, consistent distances, confirming that LLMs do not encode numbers as a continuous space. The heatmap below visualizes these pairwise cosine distances, illustrating distinct jumps at token thresholds:
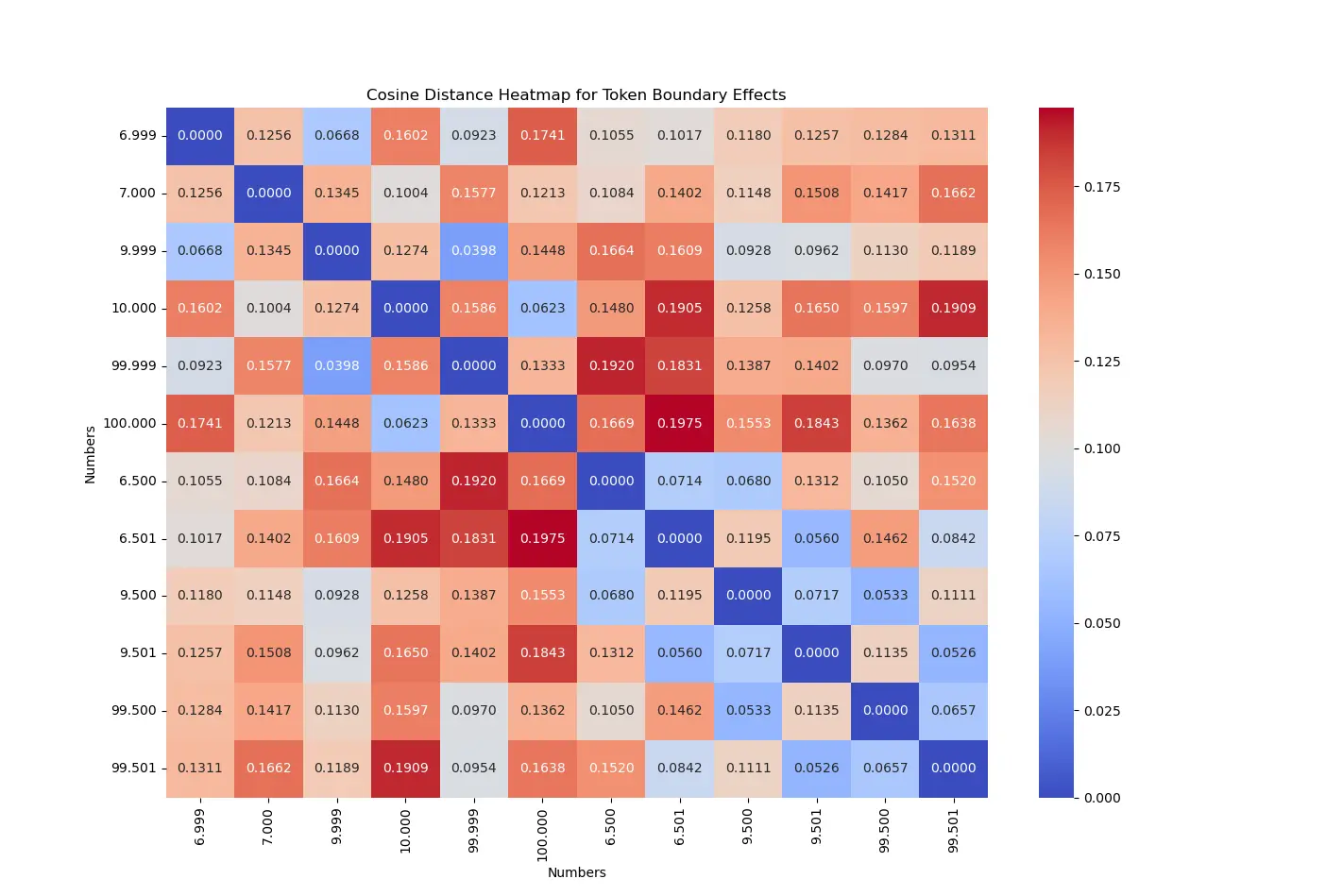
These results confirm that numbers expected to be smoothly interpolated instead exhibit embedding discontinuities. Tokenization effects create artificial segmentation in numerical representations, leading to non-linear distortions near numerical boundaries and limiting the precision of LLM-based regression models.
Key Takeaway
Discrete tokenization disrupts the continuity necessary for precise regression. Even if an LLM has a perfect internal function approximation, stepwise decoding ensures abrupt jumps, limiting its ability to represent fine-grained numerical relationships. This fundamental limitation must be considered when applying LLMs to high-precision numerical tasks.
2.4 High Bias–Variance Trade-off
The standard bias–variance decomposition in regression states:
\[\mathbb{E}\bigl[(f^*(x) - \hat{f}(x))^2\bigr] = \underbrace{\text{Bias}^2(\hat{f})}_{\text{systematic error from discretization}} + \underbrace{\mathrm{Var}(\hat{f})}_{\text{random error from sampling}} + \sigma^2.\]As discussed in Sections 2.2 and 2.3, LLMs face challenges in numerical precision due to tokenization errors (leading to bias) and probabilistic sampling (leading to variance). These factors contribute to a high bias–variance trade-off:
- High Bias: LLMs cannot perfectly represent continuous values due to discretization constraints.
- High Variance: Probabilistic token sampling introduces output instability, with small variations affecting later digits.
Lemma (Bias–Variance in Discrete Outputs)
Statement: Let \(\hat{f}(x)\) be an LLM’s discrete predictor and \(f^*(x)\) the true (continuous) function. Then:
\[\text{Bias}^2(\hat{f}) \geq \delta^2, \quad \mathrm{Var}(\hat{f}) \geq \nu^2,\]where \(\delta\) depends on tokenization granularity, and \(\nu\) is influenced by probabilistic sampling during autoregressive decoding. Both are strictly positive constants.
- \(f^*(x)\): The ideal continuous function.
- \(\hat{f}(x)\): The LLM’s discrete approximation.
- \(\delta\): Lower bound on bias from tokenization.
- \(\nu\): Lower bound on variance from sampling.
- \(\sigma^2\): Irreducible noise in the problem.
The lemma states that both the bias and variance of an LLM’s numerical predictions have strictly positive lower bounds. This means that regardless of how well an LLM is trained:
- It cannot eliminate bias because numbers are represented using discrete tokens, leading to systematic rounding errors.
- It cannot eliminate variance because each token is generated probabilistically, introducing randomness in numerical outputs.
Key Takeaway
Even when irreducible noise (\(\sigma^2\)) is minimal, LLMs remain limited by bias from discretization and variance from probabilistic decoding. This makes them less reliable for high-precision numerical tasks than traditional regression models.
Conclusion
While LLMs have made significant progress in natural language tasks, they still struggle with precise numerical regression due to tokenization errors, error accumulation in autoregressive decoding, and discontinuities in discrete outputs. These challenges create unavoidable bias and variance, making LLMs unreliable for applications that demand high numerical accuracy. However, there are ways to improve their performance, such as combining LLMs with continuous regression models, optimizing tokenization methods, and implementing self-correcting pipelines. That said, even with these adjustments, LLMs are better suited for reasoning and interpretation rather than precise numerical computation. In my next blog post, I’ll explore how we can enhance LLMs for regression to push their accuracy further.
Citation
If referencing this article, please use the following citation format:
@misc{karthick2025LLMReg,
author = {Karthick Panner Selvam},
title = {Why Large Language Models Fail at Precision Regression},
year = {2025},
date = {Feb 15, 2025},
url = {https://karthick.ai/blog/2025/LLM-Regression/},
}
References
-
Bartle, R. G., & Sherbert, D. R. (2011). Introduction to Real Analysis (4th ed.). Wiley.
-
Cover, T. M., & Thomas, J. A. (2006). Elements of Information Theory (2nd ed.). Wiley-Interscience.
-
Hastie, T., Tibshirani, R., & Friedman, J. (2009). The Elements of Statistical Learning: Data Mining, Inference, and Prediction (2nd ed.). Springer.
-
Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., Kaiser, Ł., & Polosukhin, I. (2017). Attention is All You Need. In Advances in Neural Information Processing Systems.