Learn by doing: TorchInductor Reduction Kernels
This is my second post in the “Learn by Doing: TorchInductor series”. The goal of this series is to understand torch.compile especially TorchInductor from first principles, by working through examples.
In this post, I’m going to focus on how reduction kernels are generated in TorchInductor, starting from graph lowering, moving through scheduling decisions, and finally looking at how TorchInductor decides between persistent and non-persistent reductions before generating Triton code.
I chose reductions on purpose. They show up everywhere in DL workloads. GEMM kernels are already well covered in many blogs and papers, but reductions don’t usually get the same level of attention even though they used in “attention”.
What is a reduction, and why does it matter?
In simple terms, a reduction takes a tensor and collapses one (or more) dimensions using an operation like sum, max, or mean. Formally, a reduction applies an associative operation across one or more axes, reducing the dimensionality of the tensor.
for the below example, input tensor of shape [3, 4] is reduced along axis 1 (the second dimension) using the max operation, resulting in an output tensor of shape [3, 1] because we used keepdim=True or else it will be [3].
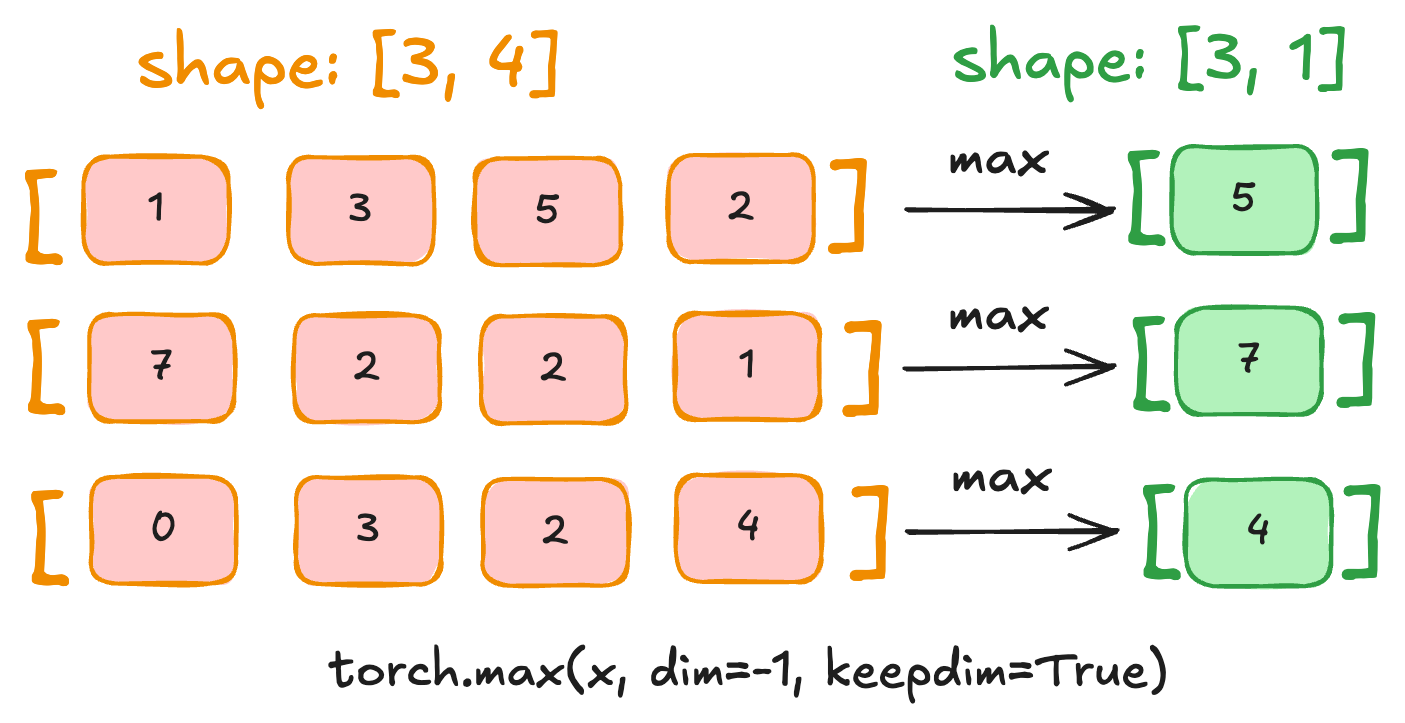
Reductions are used frequently in LLMs and other large models. For example, softmax relies on reductions to compute the maximum value for numerical stability and the sum of exponentials for normalization. LayerNorm and RMSNorm use reductions to compute statistics such as the mean and variance
We’ll use softmax as an example to understand how TorchInductor handles reductions. Softmax is a good choice because it combines multiple reduction patterns (max and sum) with elementwise ops, and it shows up frequently in many models. At a high level, softmax converts a vector of logits (unnormalized scores) into a probability distribution: all outputs are positive and sum to 1.
For a row \(x = (x_1, x_2, \dots, x_n)\), the softmax function is defined as:
\[\mathrm{softmax}(x_i) = \frac{e^{x_i - m}}{\sum_{j=1}^{n} e^{x_j - m}}, \quad \text{where } m = \max_{j} x_j\]The subtraction of \(m\) does not change the result, but it prevents numerical overflow when computing exponentials.
From a reduction perspective, this formula contains two reductions over the same dimension:
- a max reduction to compute \(m\)
- a sum reduction to compute the denominator
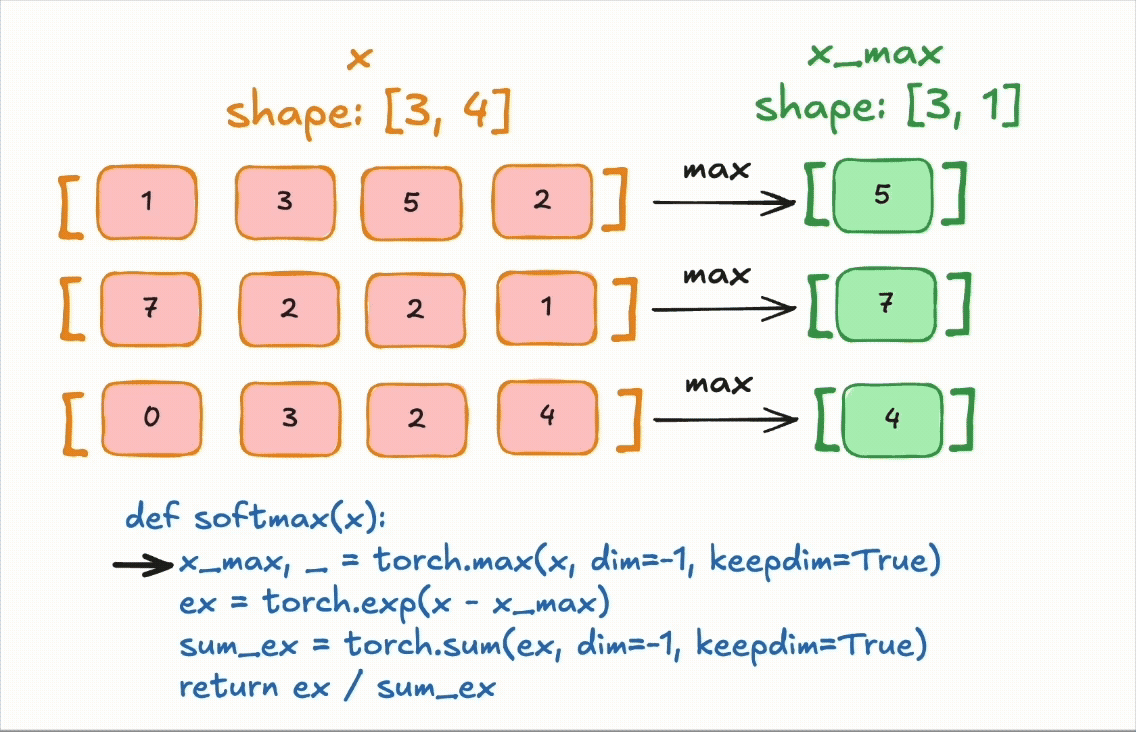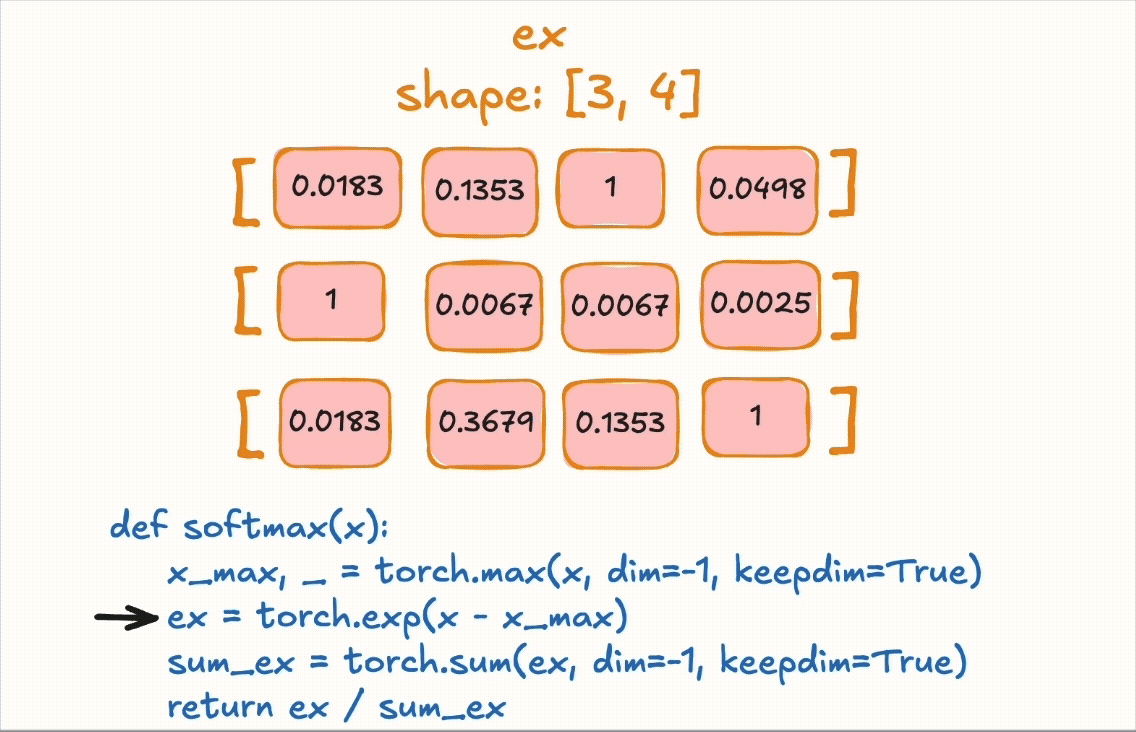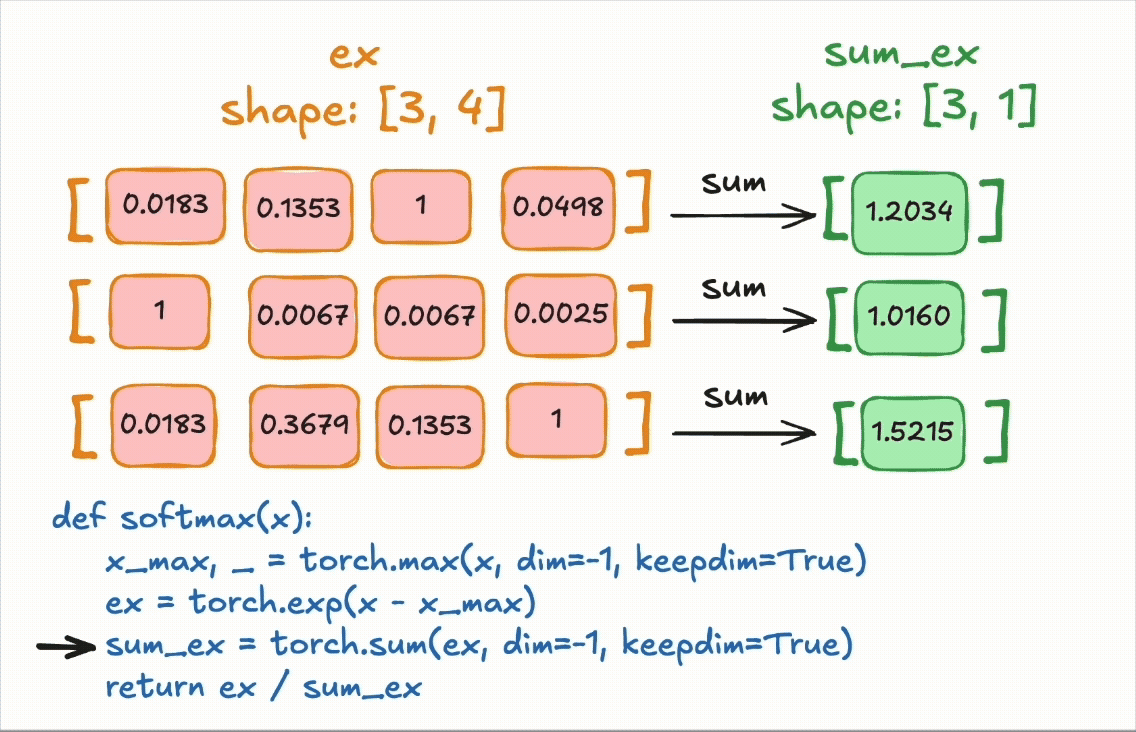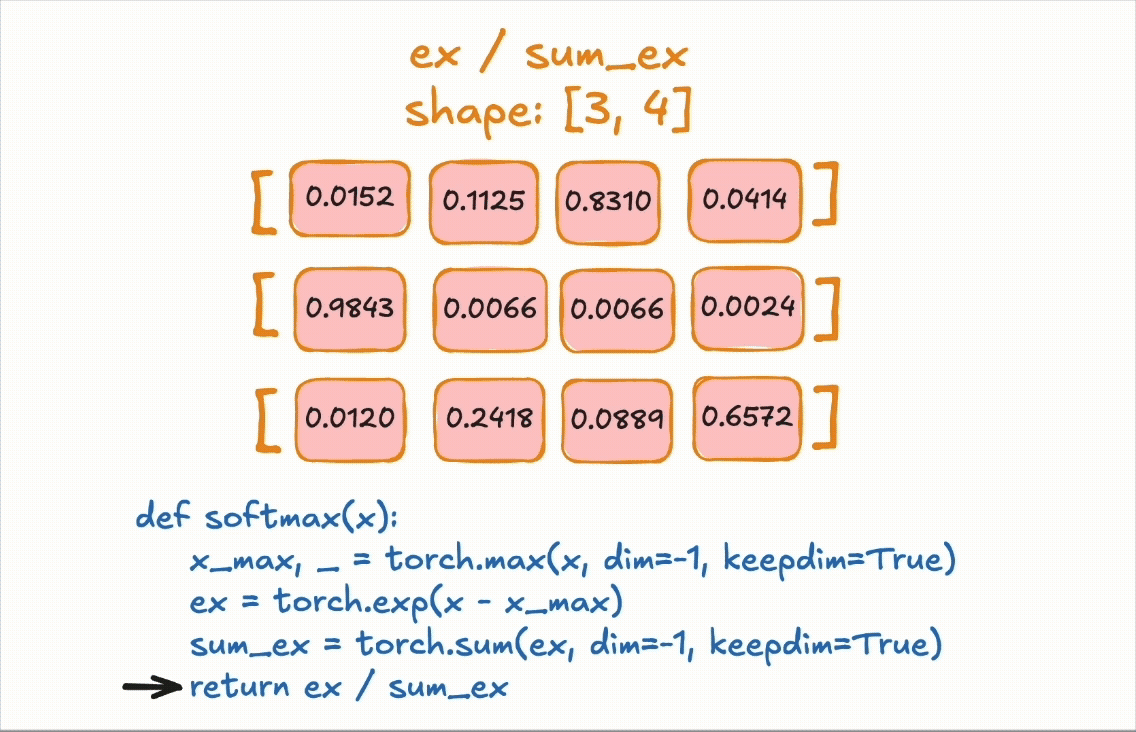
if you run the following code:
import torch
def fn(x):
return torch.softmax(x, dim=1)
x = torch.randn(4096, 1024, device="cuda")
compiled_softmax = torch.compile(fn)
out = compiled_softmax(x)
with TORCH_COMPILE_DEBUG=1 it generates intermediate compilation artifacts under torch_compile_debug/ folder. The one of the file is, fx_graph_runnable.py, is written before post_grad pass.
lets first look the fx_graph_runnable:
def forward(self, arg0_1: "f32[4096, 1024]"):
# File: reduction.py:7 in fn, code: return torch.softmax(x, dim=1)
amax: "f32[4096, 1]" = torch.ops.aten.amax.default(arg0_1, [1], True)
sub: "f32[4096, 1024]" = torch.ops.aten.sub.Tensor(arg0_1, amax); arg0_1 = amax = None
exp: "f32[4096, 1024]" = torch.ops.aten.exp.default(sub); sub = None
sum_1: "f32[4096, 1]" = torch.ops.aten.sum.dim_IntList(exp, [1], True)
div: "f32[4096, 1024]" = torch.ops.aten.div.Tensor(exp, sum_1); exp = sum_1 = None
return (div,)
In the fx_graph_runnable.py, softmax still appears in its fully decomposed form: a row-wise amax, followed by sub, exp, a row-wise sum, and finally div. At this point, Inductor is still operating on the graph produced by Dynamo and earlier lowering passes, and no softmax-specific rewrite has happened yet.
The transformation happens in the post-grad pass, inside torch/_inductor/fx_passes/post_grad.py. In this pass, Inductor explicitly looks for the softmax pattern using a pattern-matching rewrite. The softmax rewrite is registered via:
register_replacement(
prepare_softmax_pattern,
prepare_softmax_replacement,
...
)
Here, prepare_softmax_pattern describes the exact FX subgraph corresponding to the decomposed softmax (the amax → sub → exp → sum pattern), and prepare_softmax_replacement constructs a new subgraph that replaces those reductions with softmax_online (which is optimized version of softmax).
The replacement uses Inductor’s generic pattern-matching register_replacement API. During the post-grad phase, Inductor iterates over registered pattern groups and applies them to the FX graph:torch/_inductor/fx_passes/post_grad.py
for i, patterns in enumerate(pass_patterns):
GraphTransformObserver(gm, f"pass_pattern_{i}").apply_graph_pass(
patterns.apply
)
When the softmax pattern matches, the matcher rewrites the graph in place. If you insert a breakpoint or print gm.graph immediately before and after this loop, you can directly observe the transformation: the separate amax and sum reductions disappear, and the graph now contains prims.prepare_softmax_online node and it returns a tuple (max, sumexp). The following getitem nodes extract these two values, which then feed the remaining elementwise ops.
def forward(self, arg0_1: "f32[4096, 1024]"):
prepare_softmax_online_default = torch.ops.prims.prepare_softmax_online.default(arg0_1, 1)
getitem: "f32[4096, 1]" = prepare_softmax_online_default[0]
getitem_1: "f32[4096, 1]" = prepare_softmax_online_default[1]; prepare_softmax_online_default = None
sub_tensor: "f32[4096, 1024]" = torch.ops.aten.sub.Tensor(arg0_1, getitem); arg0_1 = getitem = None
exp_default: "f32[4096, 1024]" = torch.ops.aten.exp.default(sub_tensor); sub_tensor = None
# File: reduction.py:7 in fn, code: return torch.softmax(x, dim=1)
div: "f32[4096, 1024]" = torch.ops.aten.div.Tensor(exp_default, getitem_1); exp_default = getitem_1 = None
return (div,)
Pre-fusion / post-fusion IR
Show pre-fusion IR
op0: SchedulerNode(ComputedBuffer)
op0.writes = [MemoryDep('buf0', c0, {c0: 4096})]
op0.unmet_dependencies = []
op0.met_dependencies = [MemoryDep('arg0_1', c0, {c0: 4194304})]
op0.outputs = [
buf0: ComputedBuffer
buf0.layout = FixedLayout('cuda:0', torch.float32, size=[4096, 1], stride=[1, 4096])
buf0.users = [NodeUser(node=SchedulerNode(name='op2'), can_inplace=False, is_weak=False)]
]
op0.group.device = cuda:0
op0.group.iteration = (4096, 1024)
op0.sizes = ([4096], [1024])
arg0_1_layout = FixedLayout('cuda:0', torch.float32, size=[4096, 1024], stride=[1024, 1])
buf0_layout = FixedLayout('cuda:0', torch.float32, size=[4096, 1], stride=[1, 4096])
class op0_loop_body:
var_ranges = {p0: 4096, p1: 1024}
index0 = 1024*p0 + p1
index1 = p0
def body(self, ops):
get_index = self.get_index('index0')
load = ops.load('arg0_1', get_index)
reduction = ops.reduction(torch.float32, torch.float32, 'online_softmax_reduce', load)
getitem = reduction[0]
getitem_1 = reduction[1]
get_index_1 = self.get_index('index1')
store_reduction = ops.store_reduction('buf0', get_index_1, getitem)
return store_reduction
op1: SchedulerNode(ComputedBuffer)
op1.writes = [MemoryDep('buf1', c0, {c0: 4096})]
op1.unmet_dependencies = []
op1.met_dependencies = [MemoryDep('arg0_1', c0, {c0: 4194304})]
op1.outputs = [
buf1: ComputedBuffer
buf1.layout = FixedLayout('cuda:0', torch.float32, size=[4096, 1], stride=[1, 4096])
buf1.users = [NodeUser(node=SchedulerNode(name='op2'), can_inplace=False, is_weak=False)]
]
op1.group.device = cuda:0
op1.group.iteration = (4096, 1024)
op1.sizes = ([4096], [1024])
arg0_1_layout = FixedLayout('cuda:0', torch.float32, size=[4096, 1024], stride=[1024, 1])
buf1_layout = FixedLayout('cuda:0', torch.float32, size=[4096, 1], stride=[1, 4096])
class op1_loop_body:
var_ranges = {p0: 4096, p1: 1024}
index0 = 1024*p0 + p1
index1 = p0
def body(self, ops):
get_index = self.get_index('index0')
load = ops.load('arg0_1', get_index)
reduction = ops.reduction(torch.float32, torch.float32, 'online_softmax_reduce', load)
getitem = reduction[0]
getitem_1 = reduction[1]
get_index_1 = self.get_index('index1')
store_reduction = ops.store_reduction('buf1', get_index_1, getitem_1)
return store_reduction
op2: SchedulerNode(ComputedBuffer)
op2.writes = [MemoryDep('buf2', c0, {c0: 4194304})]
op2.unmet_dependencies = [MemoryDep('buf0', c0, {c0: 4096}), MemoryDep('buf1', c0, {c0: 4096})]
op2.met_dependencies = [MemoryDep('arg0_1', c0, {c0: 4194304})]
op2.outputs = [
buf2: ComputedBuffer
buf2.layout = FixedLayout('cuda:0', torch.float32, size=[4096, 1024], stride=[1024, 1])
buf2.users = [NodeUser(node=OUTPUT, can_inplace=False, is_weak=False)]
]
op2.group.device = cuda:0
op2.group.iteration = (4194304, 1)
op2.sizes = ([4096, 1024], [])
arg0_1_layout = FixedLayout('cuda:0', torch.float32, size=[4096, 1024], stride=[1024, 1])
buf0_layout = FixedLayout('cuda:0', torch.float32, size=[4096, 1], stride=[1, 4096])
buf1_layout = FixedLayout('cuda:0', torch.float32, size=[4096, 1], stride=[1, 4096])
buf2_layout = FixedLayout('cuda:0', torch.float32, size=[4096, 1024], stride=[1024, 1])
class op2_loop_body:
var_ranges = {p0: 4096, p1: 1024}
index0 = 1024*p0 + p1
index1 = p0
def body(self, ops):
get_index = self.get_index('index0')
load = ops.load('arg0_1', get_index)
get_index_1 = self.get_index('index1')
load_1 = ops.load('buf0', get_index_1)
sub = ops.sub(load, load_1)
exp = ops.exp(sub)
get_index_2 = self.get_index('index1')
load_2 = ops.load('buf1', get_index_2)
truediv = ops.truediv(exp, load_2)
get_index_3 = self.get_index('index0')
store = ops.store('buf2', get_index_3, truediv, None)
return store
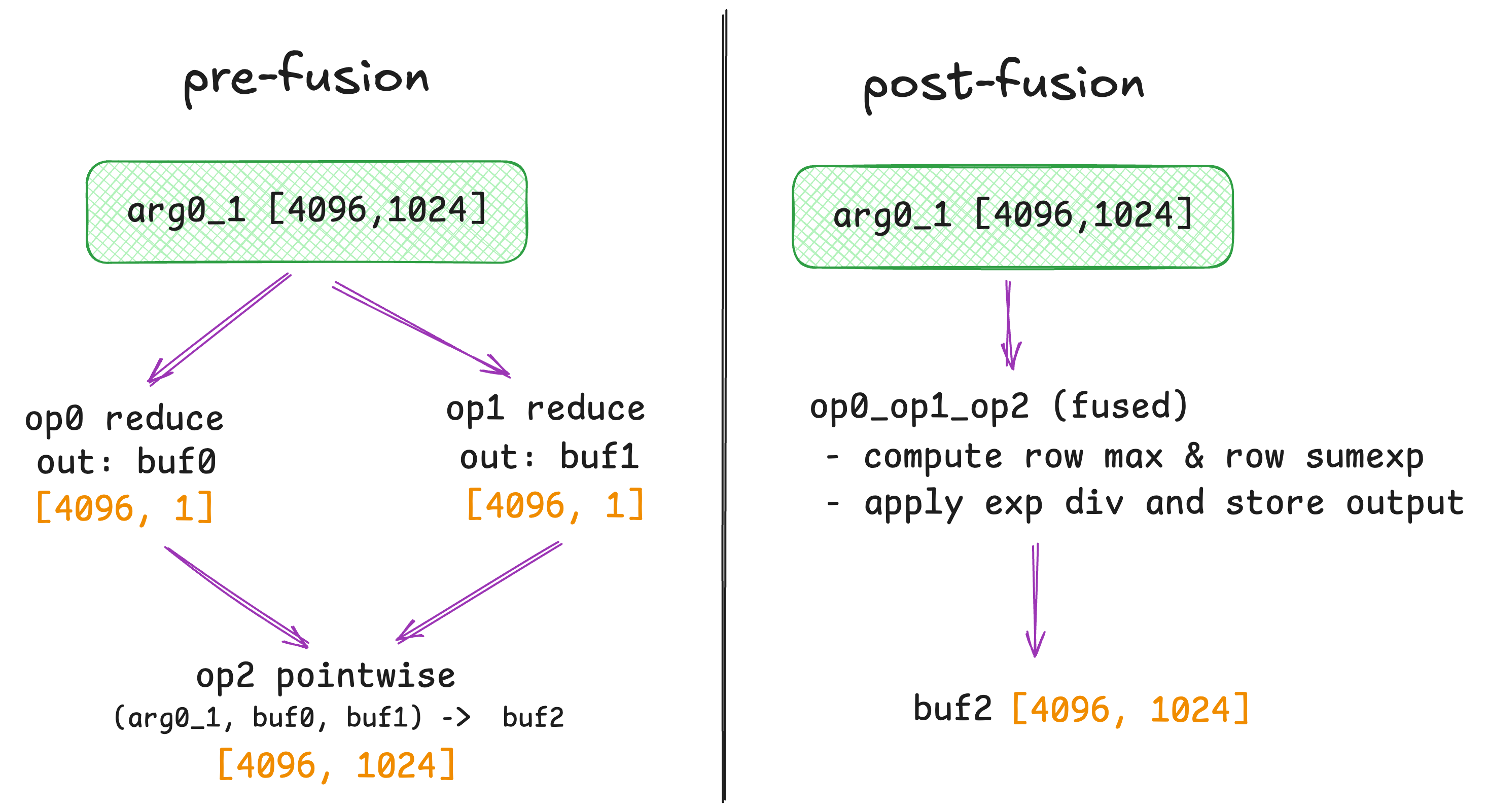
Before fusion, Inductor represents softmax as three separate scheduler nodes. Each node produces a buffer, and the dependencies force an execution order.
-
op0: reducesarg0_1across the inner dimension and writesbuf0with shape [4096, 1] -
op1: does the same reduction and writesbuf1with shape [4096, 1] -
op2: readsarg0_1,buf0, andbuf1and writes the final outputbuf2with shape [4096, 1024]
The important part is the dependency chain: op0 and op1 depend only on arg0_1 op2 has unmet dependencies on buf0 and buf1, so it cannot run until both reductions finish.
Show post-fusion IR
op0_op1_op2: FusedSchedulerNode(SchedulerNode,SchedulerNode,SchedulerNode)
op0_op1_op2.writes =
[ MemoryDep('buf0', c0, {c0: 4096}),
MemoryDep('buf1', c0, {c0: 4096}),
MemoryDep('buf2', c0, {c0: 4194304})]
op0_op1_op2.unmet_dependencies = []
op0_op1_op2.met_dependencies = [MemoryDep('arg0_1', c0, {c0: 4194304})]
op0_op1_op2.outputs = [
buf0: ComputedBuffer
buf0.layout = FixedLayout('cuda:0', torch.float32, size=[4096, 1], stride=[1, 4096])
buf0.users = [NodeUser(node=SchedulerNode(name='op2'), can_inplace=False, is_weak=False)]
buf1: ComputedBuffer
buf1.layout = FixedLayout('cuda:0', torch.float32, size=[4096, 1], stride=[1, 4096])
buf1.users = [NodeUser(node=SchedulerNode(name='op2'), can_inplace=False, is_weak=False)]
buf2: ComputedBuffer
buf2.layout = FixedLayout('cuda:0', torch.float32, size=[4096, 1024], stride=[1024, 1])
buf2.users = [NodeUser(node=OUTPUT, can_inplace=False, is_weak=False)]
]
op0_op1_op2.snodes[0] =
op0: SchedulerNode(ComputedBuffer)
op0.writes = [MemoryDep('buf0', c0, {c0: 4096})]
op0.unmet_dependencies = []
op0.met_dependencies = [MemoryDep('arg0_1', c0, {c0: 4194304})]
op0.outputs = [
buf0: ComputedBuffer
buf0.layout = FixedLayout('cuda:0', torch.float32, size=[4096, 1], stride=[1, 4096])
buf0.users = [NodeUser(node=SchedulerNode(name='op2'), can_inplace=False, is_weak=False)]
]
op0.group.device = cuda:0
op0.group.iteration = (4096, 1024)
op0.sizes = ([4096], [1024])
arg0_1_layout = FixedLayout('cuda:0', torch.float32, size=[4096, 1024], stride=[1024, 1])
buf0_layout = FixedLayout('cuda:0', torch.float32, size=[4096, 1], stride=[1, 4096])
class op0_loop_body:
var_ranges = {p0: 4096, p1: 1024}
index0 = 1024*p0 + p1
index1 = p0
def body(self, ops):
get_index = self.get_index('index0')
load = ops.load('arg0_1', get_index)
reduction = ops.reduction(torch.float32, torch.float32, 'online_softmax_reduce', load)
getitem = reduction[0]
getitem_1 = reduction[1]
get_index_1 = self.get_index('index1')
store_reduction = ops.store_reduction('buf0', get_index_1, getitem)
return store_reduction
op0_op1_op2.snodes[1] =
op1: SchedulerNode(ComputedBuffer)
op1.writes = [MemoryDep('buf1', c0, {c0: 4096})]
op1.unmet_dependencies = []
op1.met_dependencies = [MemoryDep('arg0_1', c0, {c0: 4194304})]
op1.outputs = [
buf1: ComputedBuffer
buf1.layout = FixedLayout('cuda:0', torch.float32, size=[4096, 1], stride=[1, 4096])
buf1.users = [NodeUser(node=SchedulerNode(name='op2'), can_inplace=False, is_weak=False)]
]
op1.group.device = cuda:0
op1.group.iteration = (4096, 1024)
op1.sizes = ([4096], [1024])
arg0_1_layout = FixedLayout('cuda:0', torch.float32, size=[4096, 1024], stride=[1024, 1])
buf1_layout = FixedLayout('cuda:0', torch.float32, size=[4096, 1], stride=[1, 4096])
class op1_loop_body:
var_ranges = {p0: 4096, p1: 1024}
index0 = 1024*p0 + p1
index1 = p0
def body(self, ops):
get_index = self.get_index('index0')
load = ops.load('arg0_1', get_index)
reduction = ops.reduction(torch.float32, torch.float32, 'online_softmax_reduce', load)
getitem = reduction[0]
getitem_1 = reduction[1]
get_index_1 = self.get_index('index1')
store_reduction = ops.store_reduction('buf1', get_index_1, getitem_1)
return store_reduction
op0_op1_op2.snodes[2] =
op2: SchedulerNode(ComputedBuffer)
op2.writes = [MemoryDep('buf2', c0, {c0: 4194304})]
op2.unmet_dependencies = [MemoryDep('buf0', c0, {c0: 4096}), MemoryDep('buf1', c0, {c0: 4096})]
op2.met_dependencies = [MemoryDep('arg0_1', c0, {c0: 4194304})]
op2.outputs = [
buf2: ComputedBuffer
buf2.layout = FixedLayout('cuda:0', torch.float32, size=[4096, 1024], stride=[1024, 1])
buf2.users = [NodeUser(node=OUTPUT, can_inplace=False, is_weak=False)]
]
op2.group.device = cuda:0
op2.group.iteration = (4194304, 1)
op2.sizes = ([4096, 1024], [])
arg0_1_layout = FixedLayout('cuda:0', torch.float32, size=[4096, 1024], stride=[1024, 1])
buf0_layout = FixedLayout('cuda:0', torch.float32, size=[4096, 1], stride=[1, 4096])
buf1_layout = FixedLayout('cuda:0', torch.float32, size=[4096, 1], stride=[1, 4096])
buf2_layout = FixedLayout('cuda:0', torch.float32, size=[4096, 1024], stride=[1024, 1])
class op2_loop_body:
var_ranges = {p0: 4096, p1: 1024}
index0 = 1024*p0 + p1
index1 = p0
def body(self, ops):
get_index = self.get_index('index0')
load = ops.load('arg0_1', get_index)
get_index_1 = self.get_index('index1')
load_1 = ops.load('buf0', get_index_1)
sub = ops.sub(load, load_1)
exp = ops.exp(sub)
get_index_2 = self.get_index('index1')
load_2 = ops.load('buf1', get_index_2)
truediv = ops.truediv(exp, load_2)
get_index_3 = self.get_index('index0')
store = ops.store('buf2', get_index_3, truediv, None)
return store
After fusion, Inductor merges these three nodes into a single op0_op1_op2: FusedSchedulerNode(op0, op1, op2): The key change is visible in the dependency metadata: op0_op1_op2.met_dependencies = [arg0_1] op0_op1_op2.unmet_dependencies = []. In other words, the scheduler now treats the whole softmax as one kernel that depends only on the input.
After the fusion: choosing persistent vs non-persistent reduction
Once Inductor has fused the softmax subgraph into a single schedulable unit, it calls should_use_persistent_reduction(...) in torch/_inductor/choices.py to choose between a persistent and a non-persistent reduction strategy. This decision is guided primarily by the reduction hint, which describes where the reduction axis sits in the iteration space.
In our case the hint is ReductionHint.INNER, meaning the reduction happens over the innermost (contiguous) dimension of the tensor. For a row-major [M, N] tensor, this corresponds to reducing over N. INNER reductions are the best case for persistent kernels because a single Triton program can often load the full reduction axis and compute the result without an explicit loop.
The heuristic allows persistent reduction for INNER reductions when the reduction size is at most 1024 elements, and only if config.triton.persistent_reductions is enabled. For our softmax with (M=4096, N=1024), the reduction axis length is exactly 1024, so Inductor selects the persistent reduction path.
For non-INNER reductions (for example, reductions over a strided outer dimension such as M), the heuristic is more conservative. In these cases, Inductor only considers persistent reduction if it can statically bound (size know at compile time) the reduction size. If the reduction size depends on runtime values or has a wide range of possible sizes, persistent reduction is rejected. This is because persistent kernels force the reduction tile size to match the maximum reduction length; if the actual size is smaller, large portions of the tile would be masked off, wasting registers and memory bandwidth.
When multi_kernel is enabled, Inductor becomes more aggressive and allows persistent reductions more often, relying on runtime benchmarking to select the faster implementation. Even in that mode, persistence is only chosen when Inductor can prove that the reduction size is finite and stays within a safe threshold. This makes that persistent reductions are used only when they are likely to improve performance, and avoided when they would introduce excessive masking or register pressure.
This is why softmax over N=1024 ends up with a persistent kernel, while larger or non-contiguous reductions fall back to the looped (non-persistent) strategy.
Generated persistent reduction kernel
@triton.jit
def triton_per_fused__softmax_exp_prepare_softmax_online_sub_0(in_ptr0, out_ptr2, xnumel, r0_numel, XBLOCK : tl.constexpr):
xnumel = 4096
r0_numel = 1024
R0_BLOCK: tl.constexpr = 1024
rnumel = r0_numel
RBLOCK: tl.constexpr = R0_BLOCK
xoffset = tl.program_id(0) * XBLOCK
xindex = xoffset + tl.arange(0, XBLOCK)[:, None] # [XBLOCK, 1]
xmask = tl.full([XBLOCK, R0_BLOCK], True, tl.int1)
r0_index = tl.arange(0, R0_BLOCK)[None, :] # [1, 1024]
r0_offset = 0
r0_mask = tl.full([XBLOCK, R0_BLOCK], True, tl.int1)
roffset = r0_offset
rindex = r0_index
r0_1 = r0_index
x0 = xindex
# Load a [XBLOCK, 1024] tile: full row(s) for each program instance
# Row-major: offset = row*1024 + col
tmp0 = tl.load(in_ptr0 + (r0_1 + 1024*x0), None) # [XBLOCK, 1024]
tmp1 = tl.broadcast_to(tmp0, [XBLOCK, R0_BLOCK])
tmp3 = tl.broadcast_to(tmp1, [XBLOCK, R0_BLOCK])
# Per-row max over the 1024 columns -> [XBLOCK, 1]
tmp5 = triton_helpers.max2(tmp3, 1)[:, None].to(tl.float32)
# exp(x - max)
tmp6 = tmp1 - tmp5
tmp7 = libdevice.exp(tmp6) # [XBLOCK, 1024]
tmp8 = tl.broadcast_to(tmp7, [XBLOCK, R0_BLOCK])
# Per-row sum(exp(x - max)) -> [XBLOCK, 1] (softmax denominator)
tmp10 = tl.sum(tmp8, 1)[:, None].to(tl.float32)
# Normalize and store
tmp11 = tmp0 - tmp5
tmp12 = libdevice.exp(tmp11)
tmp13 = (tmp12 / tmp10)
tl.store(out_ptr2 + (r0_1 + 1024*x0), tmp13, None)
This kernel is “persistent” because the full reduction axis fits inside one program instance. Here r0_numel = 1024 and R0_BLOCK = 1024, so the program loads the entire row tile for each row it owns. The indexing expression (r0_1 + 1024 * x0) is simply row-major addressing for a [4096, 1024] tensor: the row stride is 1024, so element (row, col) lives at row * 1024 + col.
xindex selects the rows owned by the current triton program (a block of XBLOCK rows), and r0_index enumerates all columns 0..1023. Broadcasting between x0 shaped [XBLOCK, 1] and r0_1 shaped [1, 1024] produces a full [XBLOCK, 1024] grid of pointers, so tl.load returns a [XBLOCK, 1024] tile in registers.
Once the tile is loaded, the kernel computes the two softmax reductions directly. tmp5 = max2(tmp3, 1) reduces across the column dimension (axis 1) and produces a per-row max of shape [XBLOCK, 1]. Subtracting tmp5 from the tile and exponentiating yields exp(x - max) for each element. tmp10 = tl.sum(..., 1) then reduces those exponentials across columns and produces the per-row denominator sum(exp(x - max)), also shaped [XBLOCK, 1]. Finally the kernel computes exp(x - max) / sumexp elementwise and stores the result back to out_ptr2 using the same row-major pointer arithmetic.
Persistent reductions keep a large working set live within a single program instance. When the reduction axis gets larger than what the heuristic allows (or register pressure becomes too high), Inductor switches to a non-persistent strategy. Even for this shape, you can force the non-persistent path by disabling persistent reductions via config.triton.persistent_reductions = False.
Generated looped reduction kernel (non persistent_reduction)
def triton_red_fused__softmax_exp_prepare_softmax_online_sub_0(in_ptr0, out_ptr2, xnumel, r0_numel, XBLOCK : tl.constexpr, R0_BLOCK : tl.constexpr):
xnumel = 4096
r0_numel = 1024
rnumel = r0_numel
RBLOCK: tl.constexpr = R0_BLOCK
xoffset = tl.program_id(0) * XBLOCK
xindex = xoffset + tl.arange(0, XBLOCK)[:, None] # [XBLOCK, 1]
xmask = tl.full([XBLOCK, R0_BLOCK], True, tl.int1)
r0_base = tl.arange(0, R0_BLOCK)[None, :] # [1, R0_BLOCK]
rbase = r0_base
x0 = xindex
# Running state for online softmax
_tmp2_max = tl.full([XBLOCK, R0_BLOCK], float('-inf'), tl.float32)
_tmp2_sum = tl.zeros([XBLOCK, R0_BLOCK], tl.float32)
# Pass 1: stream tiles to compute (final_max, final_sumexp)
for r0_offset in range(0, r0_numel, R0_BLOCK):
r0_index = r0_offset + r0_base
r0_mask = r0_index < r0_numel
roffset = r0_offset
rindex = r0_index
r0_1 = r0_index
tmp0 = tl.load(in_ptr0 + (r0_1 + 1024*x0), r0_mask, eviction_policy='evict_last', other=0.0)
tmp1 = tl.broadcast_to(tmp0, [XBLOCK, R0_BLOCK])
_tmp2_max_next, _tmp2_sum_next = triton_helpers.online_softmax_combine(
_tmp2_max, _tmp2_sum, tmp1, False
)
_tmp2_max = tl.where(r0_mask, _tmp2_max_next, _tmp2_max)
_tmp2_sum = tl.where(r0_mask, _tmp2_sum_next, _tmp2_sum)
tmp2, tmp3 = triton_helpers.online_softmax_reduce(
_tmp2_max, _tmp2_sum, 1, False)
tmp2 = tmp2[:, None] # final_max, [XBLOCK, 1]
tmp3 = tmp3[:, None] # final_sumexp, [XBLOCK, 1]
# Pass 2: reload tiles, normalize, store
for r0_offset in range(0, r0_numel, R0_BLOCK):
r0_index = r0_offset + r0_base
r0_mask = r0_index < r0_numel
roffset = r0_offset
rindex = r0_index
r0_1 = r0_index
tmp4 = tl.load(in_ptr0 + (r0_1 + 1024*x0), r0_mask, eviction_policy='evict_first', other=0.0) # [XBLOCK, R0_BLOCK]
tmp5 = tmp4 - tmp2 # x - final_max
tmp6 = libdevice.exp(tmp5) # exp(x - max)
tmp7 = (tmp6 / tmp3) # / final_sumexp
tl.store(out_ptr2 + (r0_1 + 1024*x0), tmp7, r0_mask)
This kernel is structured around chunking the reduction axis into tiles of size R0_BLOCK. The same row-major addressing is used (row * 1024 + col), but unlike the persistent kernel it does not assume that the full row fits in one tile. Instead it explicitly loops over r0_offset and processes columns in blocks [r0_offset : r0_offset + R0_BLOCK).
The first loop computes the softmax statistics using the online formulation. _tmp2_max and _tmp2_sum represent a running (max, sumexp) state. For each tile, the kernel loads a [XBLOCK, R0_BLOCK] block of the input and calls online_softmax_combine. After all tiles are processed, online_softmax_reduce collapses the running state across the column dimension and returns two per-row scalars: tmp2 is the final max, and tmp3 is the final denominator sum(exp(x - max)), both shaped [XBLOCK, 1].
The second loop performs the actual normalization. It reloads the same input tiles (because the output requires per-element exponentials), computes exp(x - tmp2) / tmp3, and stores the result. The tl.load take an eviction_policy hint (e.g., “evict_first” or “evict_last”) that changes the NVIDIA PTX cache eviction policy. In NVIDIA PTX, evict_first means the line is likely evicted first (good for streaming), while evict_last means it’s evicted last (good for data to persist in cache), thats why first pass used the evict_last and second pass used evict_first.
In practice, persistent reduction tends to win when the reduction axis is small enough to fit comfortably in a single tile, because it avoids the explicit reduction loop. The non-persistent path is more general and scales to larger reduction sizes, but it pays for that generality with extra loop structure and typically higher memory traffic.
Performance comparison
To compare persistent vs non-persistent reductions, I ran the torch.softmax(x, dim=1) under two modes. In default, Inductor follows should_use_persistent_reduction and picks persistent or non-persistent based on the heuristic. In force_reduction, I disable persistent reductions using this flag config.triton.persistent_reductions = False so Inductor always generates the non-persistent (looped) kernel.
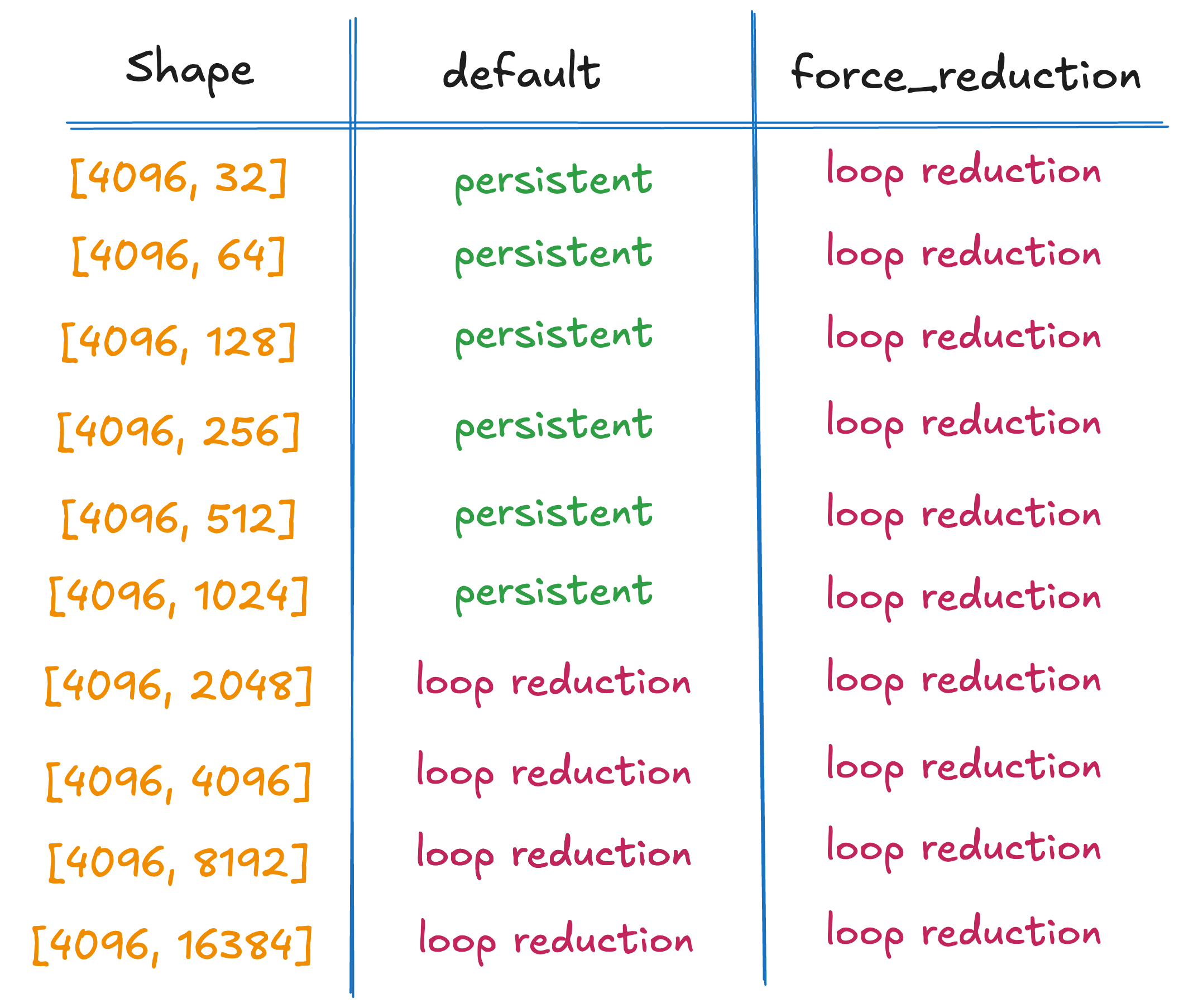
The table below summarizes which kernel type each mode uses for M=4096 across the sweep. In default, sizes N=32..1024 use the persistent kernel and force_reduction uses non-persistent for every N. (there are few ways to check generated kernel is persistent or not, we can use TORCH_LOGS="output_code" or TORCH_COMPILE_DEBUG=1 inspect manually triton code. We can also verify this from profiling output (PyTorch profiler or ncu) by looking at the kernel name, kernels starting with triton_per are persistent, while those starting with triton_red are the non-persistent reduction path.)
I collected performance data with Nsight Compute ncu, and extracted two metrics: sm__cycles_elapsed.avg (SM cycles) and gpu__time_duration.avg (kernel duration). The plots show a clear advantage for default from N=32 up to N=1024. Past that point, the curves largely overlap because default also switches to the non-persistent path for larger N.
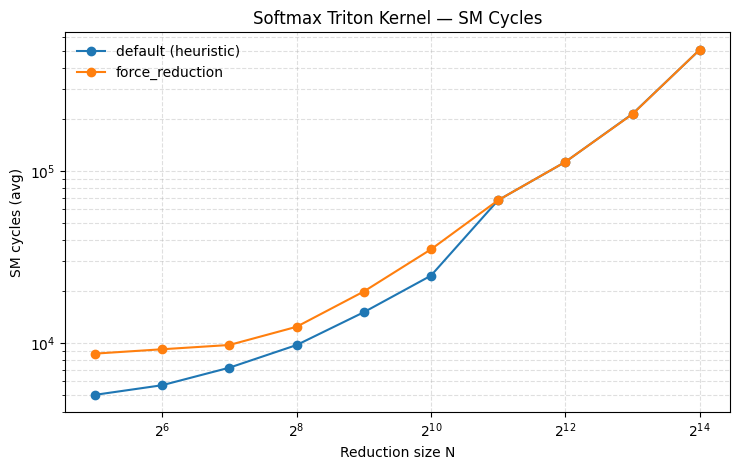
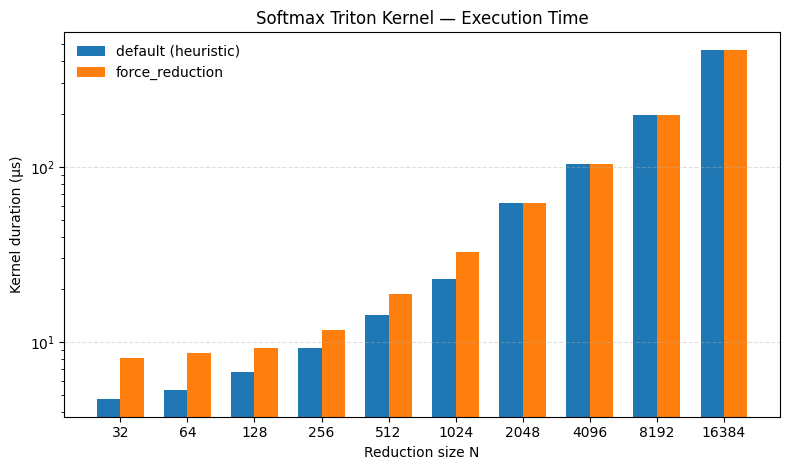
The speedup in the persistent region comes from how the kernel is structured. The persistent softmax kernel can load the full reduction axis in one tile, compute the row max and row sum, and write the output, so it effectively does one global read of the input and one global write of the output. The non-persistent kernel computes the softmax statistics in a first pass and then reloads the input to write the normalized output, so it ends up doing multiple global reads and global write, plus additional work to maintain the running (max, sum) state. That shows up directly in the higher SM cycle counts.
Persistent reduction isn’t always available, though. As N grows, keeping a full row tile and its intermediates live increases register pressure, which can reduce occupancy or even make the kernel infeasible. That’s why Inductor’s heuristic stops using persistent reductions beyond a threshold and falls back to the looped reduction strategy. You can find the benchmark script used for this sweep in reduction.py and run.sh. I ran it on colab with A100 GPU (torch 2.9.0+cu126).
Thanks for reading. I hope this post helped clarify how TorchInductor generates reduction kernels and why choices like persistent vs non-persistent matter. If you’re interested in contributing to PyTorch, browsing issues tagged good first issue link is a solid place to start.
Happy coding, and happy new year 2026 🎉.
References
-
https://github.com/pytorch/pytorch
-
https://triton-lang.org/main/index.html